Haben Sie sich jemals gefragt, welcher Algorithmus im Herzen vieler innovativer maschineller Lernmodelle arbeitet? Der Gradientenabstieg ist die Antwort. Er ist ein mächtiger Optimierungsalgorithmus, fundamental für Optimierungen basierend auf Daten und das Training künstlicher Intelligenz-Modelle.
Dieser Algorithmus spielt eine Schlüsselrolle bei der Minimierung von Kostenfunktionen. Er findet optimale Lösungen für komplexe Herausforderungen. In Bereichen wie Finanzen, Gesundheitswesen und fortschrittlicher Technologie wird der Gradientenabstieg genutzt.
Er ermöglicht präzise Vorhersagen und Entscheidungen, gestützt auf große Datenmengen. Aber wie funktioniert dieser Stützpfeiler des maschinellen Lernens genau, und was macht ihn so essentiell?
Einführung in den Gradientenabstieg
Der Gradientenabstiegsverfahren ist ein grundlegender Bestandteil der modernen Lernalgorithmen. Es spielt eine entscheidende Rolle im Bereich des maschinellen Lernens. Dieses Verfahren zielt darauf ab, das Minimum einer Funktion zu finden. Es schreitet iterativ in die Richtung des steilsten Abstiegs fort. Doch was verbirgt sich hinter diesem Algorithmus und warum ist er so bedeutend?
Was ist Gradientenabstieg?
Der Gradientenabstieg ist eine Methode zur Optimierung von Funktionen. Der Algorithmus führt schrittweise in Richtung des steilsten Gefälles. Ziel ist es, den Punkt der minimalen Kostenfunktion zu finden. Dies minimiert den Fehler in einer Vorhersage.
Das Prinzip des Gradientenabstiegsverfahrens besteht darin, die Modellparameter anzupassen. Dadurch wird die Differenz zwischen den tatsächlichen und den vorhergesagten Werten verringert.
Bedeutung im maschinellen Lernen
Im maschinellen Lernen spielt der Gradientenabstieg eine zentrale Rolle. Er ist essenziell für die Anwendung von Lernalgorithmen. Durch die Optimierung der Modellparameter verbessert der Algorithmus verstehen die Vorhersagegenauigkeit. Dies geschieht durch kontinuierliches Anpassen der Parameter.
Eine präzise Anwendung dieses Verfahrens ermöglicht Modellen, schneller zu konvergieren. Dadurch liefern sie zuverlässigere Ergebnisse.
Wie funktioniert der Gradientenabstieg?
Der Kern des Gradientenabstiegs ist essentiell für zahlreiche Algorithmen im Bereich des maschinellen Lernens. Es basiert auf der Berechnung der Steigung oder Ableitung der Kostenfunktion an einem spezifischen Punkt. Anschließend erfolgt die Anpassung der Gewichte in die umgekehrte Richtung des Gradienten.
Dieser Prozess wird fortlaufend wiederholt, um die Gewichte schrittweise genauer zu justieren. Ziel ist es, ein Minimum der Kostenfunktion zu erreichen. Durch die iterative Optimierung können sowohl lokale als auch globale Minima erreicht werden. Das hängt von der Einstellung der Lernrate und weiteren Faktoren ab.
Die Schritte des Gradientenabstiegs umfassen:
- Die Berechnung der Ableitung der Kostenfunktion.
- Die Anpassung der Gewichte entgegen des Gradienten.
- Die kontinuierliche Wiederholung bis zur Annäherung an ein Optimum.
Jede Iteration verfeinert die Gewichte, um die Kostenfunktion zu minimieren.
Optimierungsalgorithmus und seine Rolle
Ein Optimierungsalgorithmus verbessert die Performance von Modellen oder Systemen. Verschiedene Strategien sind entscheidend, um Ziele effizient zu erreichen.
Was ist ein Optimierungsalgorithmus?
Er wurde entwickelt, um Effizienz und Präzision zu steigern. Durch algorithmische Optimierung findet er ideale Parameter. Solche Algorithmen spielen eine zentrale Rolle bei der Modelloptimierung. Sie sorgen für die perfekte Ausgewogenheit zwischen Genauigkeit und Komplexität.

Gradientenabstieg als Optimierungsalgorithmus
Gradientenabstieg ist eine bevorzugte Optimierungsstrategie im maschinellen Lernen. Sie passt Modellgenauigkeit fortlaufend an, um ideale Leistung zu garantieren. Dies erreicht man durch iteratives Optimieren der Modellparameter. Es minimiert die Kostenfunktion und steigert die Effizienz, was in der Modelloptimierung zentral ist.
Steigungsdreieck und seine Bedeutung
Das Steigungsdreieck ist in der Differentialrechnung unverzichtbar. Es ermöglicht die Bestimmung der Steigung einer Funktion. Dieses Werkzeug ist entscheidend, um zu verstehen, wie sich eine Funktion verändert. Im Kontext der Optimierungsmethoden ist es essentiell, um Richtung und Größe von Anpassungen festzulegen.
Definition des Steigungsdreiecks
Definiert wird es als rechtwinkliges Dreieck, bildlich dargestellt durch die Veränderung einer Funktion in einem kurzen Intervall. Die Steigung ergibt sich aus dem Verhältnis der vertikalen zu den horizontalen Änderungen. Diese Ermittlungsweise ist grundlegend für die Berechnung von Änderungsraten in der Differentialrechnung.
Anwendungsbeispiele
Im Bereich des maschinellen Lernens ist das Steigungsdreieck besonders relevant. Es wird in neuronalen Netzwerken genutzt, um während des Trainings die Modelgewichte anzupassen. Der dabei berechnete Gradient, basierend auf der Steigung, wird durch das Steigungsdreieck bestimmt. Differentialrechnung findet auch in Regressionsmodellen Anwendung, zur Ermittlung optimaler Parameter, die eine Modellkurve den Daten bestmöglich annähern.
Minimierungsalgorithmus zur Kostenfunktion
Der Gradientenabstieg ist ein leistungsfähiger Weg, die Kostenfunktion zu senken. Diese Funktion bewertet den Unterschied zwischen vorhergesagten und echten Werten. Man bezeichnet diesen Unterschied häufig als Loss-Funktion. Mit jedem Schritt des Verfahrens versucht man, dieses Missverhältnis zu verringern. Dadurch verbessert sich die Genauigkeit des Machine-Learning-Modells.
Die Hauptstärke des Gradientenabstiegs liegt in der stetigen Verringerung des Fehlers. Das kontinuierliche Minimieren der Kostenfunktion führt zu effizienterem Training von Modellen. So lassen sich genauere Vorhersagen erzielen. Die Feinjustierung der Parameter in kleinen Etappen führt zu schrittweiser Kostenreduktion. Das ermöglicht es, die beste Lösung zu finden.
Die Rolle der Ableitung im Gradientenabstieg
Im Kern des Gradientenabstiegs ist die Ableitung entscheidend, denn sie zeigt, wo es steil bergauf geht. Sie hilft bei der Bestimmung des Gradienten in der mathematischen Analyse. Dieser Gradientenvektor, bestehend aus den ersten Ableitungen, zielt immer auf den steilsten Anstieg ab.
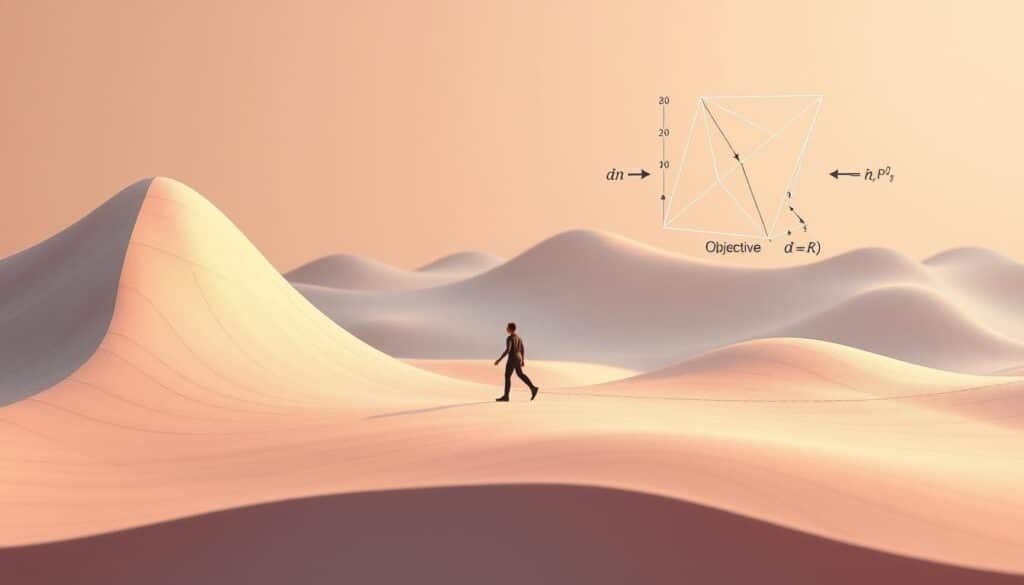
Beim Gradientenabstieg nutzen wir die entgegengesetzte Richtung dieses Gradienten. Dies hilft, das tiefste Tal der Funktion zu finden. Man bewegt sich schrittweise dorthin, wo der Abstieg am größten ist. So nähert man sich dem Minimum der Kostenfunktion an, das erreicht werden soll.
Die mathematische Analyse erlaubt uns, Ableitungen und Gradienten präzise zu berechnen. Dadurch werden die Ergebnisse genauer und die Optimierung effizienter. Offenbar ist die Ableitung unerlässlich im Gradientenabstiegsprozess.
Konvergenz und Iteration im Gradientenabstieg
Der Gradientenabstieg ist in der Welt des maschinellen Lernens unerlässlich, um durch Minimierung der Kostenfunktion optimale Parameter zu finden. Es ist von Bedeutung, Konvergenz und den Iterationsprozess zu verstehen, um den Algorithmus effektiv zu nutzen.
Was ist Konvergenz?
Konvergenz im Rahmen des Gradientenabstiegs bedeutet, einen Punkt zu erreichen, an dem weitere Iterationen die Kostenfunktion nicht wesentlich verbessern. Das zeigt an, dass eine optimale Lösung oder ein Minimum gefunden wurde. Hier spielt die Effizienz des Algorithmus eine große Rolle, denn sie bestimmt die Schnelligkeit und Genauigkeit, mit der dieser Punkt erreicht wird.
Iterative Vorgehensweise
Der Prozess des Gradientenabstiegs verbessert durch ständiges Anpassen der Parameter schrittweise das Resultat. Jede Iteration bringt den Algorithmus seinem Ziel näher, die Konvergenz zu erreichen. Dies erhöht nicht nur die Effizienz des Algorithmus, sondern auch die Qualität der Ergebnisse.
Wichtigkeit der Lernrate im Gradientenabstieg
Die Lernrate spielt eine zentrale Rolle im Gradientenabstieg, indem sie die Größe der Schritte zur Parameteraktualisierung steuert. Nur die richtige Einstellung der Lernrate führt zu einer schnellen und effizienten Konvergenz. Andernfalls könnte das Modell stagnieren, ohne signifikante Verbesserungen zu erreichen.
Lernrate festlegen
Eine angemessene Lernrate zu finden, erfordert Ausgewogenheit. Zu hohe Lernraten können Oszillationen auslösen, die den Konvergenzprozess stören. Auf der anderen Seite führt eine zu niedrige Lernrate zu einer deutlichen Verlangsamung der Konvergenz. Es ist entscheidend, verschiedene Werte zu testen und die Modellleistung zu evaluieren, um die ideale Lernrate festzulegen.
Optimale Lösung finden
Die optimale Lösung zu finden, benötigt Geduld und eine systematische Herangehensweise. Eine sorgfältige Performance-Evaluierung hilft dabei zu verstehen, wie verschiedene Lernraten die Ergebnisse beeinflussen. Die korrekte Justierung der Lernrate als Hyperparameter ist entscheidend für die Leistungssteigerung des Modells.
Fazit
Wir haben den enormen Einfluss des Gradientenabstiegs auf die Effektivität maschineller Lernalgorithmen beleuchtet. Dieser Optimierungsalgorithmus ist entscheidend für die Erstellung präziser Modelle. Solche Modelle sind fähig, genaue Vorhersagen zu machen. Das Verständnis und die korrekte Anwendung dieses Algorithmus sind daher für Innovationen im maschinellen Lernen unerlässlich.
Die Stärke des Gradientenabstiegs liegt darin, Kostenfunktionen effizient zu minimieren und Modelle fortlaufend zu verfeinern. Die Bedeutung der Ableitung und der angemessenen Einstellung der Lernrate sind dabei nicht zu unterschätzen. Diese Elemente sind zentral für die Konvergenz und Verbesserung der Modelle. Eine gut angepasste Lernrate hebt die Effizienz und Wirksamkeit der Lernmodelle hervor.
Somit bleibt der Gradientenabstieg ein zentrales Instrument in der KI-Forschung und -Entwicklung. Durch die gezielte Anwendung dieser Methodik können Datenwissenschaftler das Potenzial ihrer Modelle voll ausschöpfen. Damit treiben sie konstante Innovationen im Bereich des maschinellen Lernens voran. Die fachgerechte Nutzung dieses Algorithmus ist und bleibt ein Schlüsselfaktor für die Entwicklung leistungsfähiger Vorhersagemodelle.
FAQ
Q: Was ist Gradientenabstieg?
Q: Welche Rolle spielt Gradientenabstieg im maschinellen Lernen?
Q: Wie funktioniert der Gradientenabstieg?
Q: Was ist ein Optimierungsalgorithmus?
Q: Wie wird Gradientenabstieg als Optimierungsalgorithmus genutzt?
Q: Was ist das Steigungsdreieck?
Q: Welche Anwendungsbeispiele gibt es für das Steigungsdreieck?
Q: Was ist ein Minimierungsalgorithmus zur Kostenfunktion?
Q: Welche Rolle spielt die Ableitung im Gradientenabstieg?
Q: Was bedeutet Konvergenz im Gradientenabstieg?
Q: Wie funktioniert die iterative Vorgehensweise im Gradientenabstieg?
Q: Warum ist die Lernrate im Gradientenabstieg wichtig?
Q: Wie findet man die optimale Lösung im Gradientenabstieg?
Haben Sie sich jemals gefragt, welcher Algorithmus im Herzen vieler innovativer maschineller Lernmodelle arbeitet? Der Gradientenabstieg ist die Antwort. Er ist ein mächtiger Optimierungsalgorithmus, fundamental für Optimierungen basierend auf Daten und das Training künstlicher Intelligenz-Modelle.
Dieser Algorithmus spielt eine Schlüsselrolle bei der Minimierung von Kostenfunktionen. Er findet optimale Lösungen für komplexe Herausforderungen. In Bereichen wie Finanzen, Gesundheitswesen und fortschrittlicher Technologie wird der Gradientenabstieg genutzt.
Er ermöglicht präzise Vorhersagen und Entscheidungen, gestützt auf große Datenmengen. Aber wie funktioniert dieser Stützpfeiler des maschinellen Lernens genau, und was macht ihn so essentiell?
Einführung in den Gradientenabstieg
Der Gradientenabstiegsverfahren ist ein grundlegender Bestandteil der modernen Lernalgorithmen. Es spielt eine entscheidende Rolle im Bereich des maschinellen Lernens. Dieses Verfahren zielt darauf ab, das Minimum einer Funktion zu finden. Es schreitet iterativ in die Richtung des steilsten Abstiegs fort. Doch was verbirgt sich hinter diesem Algorithmus und warum ist er so bedeutend?
Was ist Gradientenabstieg?
Der Gradientenabstieg ist eine Methode zur Optimierung von Funktionen. Der Algorithmus führt schrittweise in Richtung des steilsten Gefälles. Ziel ist es, den Punkt der minimalen Kostenfunktion zu finden. Dies minimiert den Fehler in einer Vorhersage.
Das Prinzip des Gradientenabstiegsverfahrens besteht darin, die Modellparameter anzupassen. Dadurch wird die Differenz zwischen den tatsächlichen und den vorhergesagten Werten verringert.
Bedeutung im maschinellen Lernen
Im maschinellen Lernen spielt der Gradientenabstieg eine zentrale Rolle. Er ist essenziell für die Anwendung von Lernalgorithmen. Durch die Optimierung der Modellparameter verbessert der Algorithmus verstehen die Vorhersagegenauigkeit. Dies geschieht durch kontinuierliches Anpassen der Parameter.
Eine präzise Anwendung dieses Verfahrens ermöglicht Modellen, schneller zu konvergieren. Dadurch liefern sie zuverlässigere Ergebnisse.
Wie funktioniert der Gradientenabstieg?
Der Kern des Gradientenabstiegs ist essentiell für zahlreiche Algorithmen im Bereich des maschinellen Lernens. Es basiert auf der Berechnung der Steigung oder Ableitung der Kostenfunktion an einem spezifischen Punkt. Anschließend erfolgt die Anpassung der Gewichte in die umgekehrte Richtung des Gradienten.
Dieser Prozess wird fortlaufend wiederholt, um die Gewichte schrittweise genauer zu justieren. Ziel ist es, ein Minimum der Kostenfunktion zu erreichen. Durch die iterative Optimierung können sowohl lokale als auch globale Minima erreicht werden. Das hängt von der Einstellung der Lernrate und weiteren Faktoren ab.
Die Schritte des Gradientenabstiegs umfassen:
- Die Berechnung der Ableitung der Kostenfunktion.
- Die Anpassung der Gewichte entgegen des Gradienten.
- Die kontinuierliche Wiederholung bis zur Annäherung an ein Optimum.
Jede Iteration verfeinert die Gewichte, um die Kostenfunktion zu minimieren.
Optimierungsalgorithmus und seine Rolle
Ein Optimierungsalgorithmus verbessert die Performance von Modellen oder Systemen. Verschiedene Strategien sind entscheidend, um Ziele effizient zu erreichen.
Was ist ein Optimierungsalgorithmus?
Er wurde entwickelt, um Effizienz und Präzision zu steigern. Durch algorithmische Optimierung findet er ideale Parameter. Solche Algorithmen spielen eine zentrale Rolle bei der Modelloptimierung. Sie sorgen für die perfekte Ausgewogenheit zwischen Genauigkeit und Komplexität.

Gradientenabstieg als Optimierungsalgorithmus
Gradientenabstieg ist eine bevorzugte Optimierungsstrategie im maschinellen Lernen. Sie passt Modellgenauigkeit fortlaufend an, um ideale Leistung zu garantieren. Dies erreicht man durch iteratives Optimieren der Modellparameter. Es minimiert die Kostenfunktion und steigert die Effizienz, was in der Modelloptimierung zentral ist.
Steigungsdreieck und seine Bedeutung
Das Steigungsdreieck ist in der Differentialrechnung unverzichtbar. Es ermöglicht die Bestimmung der Steigung einer Funktion. Dieses Werkzeug ist entscheidend, um zu verstehen, wie sich eine Funktion verändert. Im Kontext der Optimierungsmethoden ist es essentiell, um Richtung und Größe von Anpassungen festzulegen.
Definition des Steigungsdreiecks
Definiert wird es als rechtwinkliges Dreieck, bildlich dargestellt durch die Veränderung einer Funktion in einem kurzen Intervall. Die Steigung ergibt sich aus dem Verhältnis der vertikalen zu den horizontalen Änderungen. Diese Ermittlungsweise ist grundlegend für die Berechnung von Änderungsraten in der Differentialrechnung.
Anwendungsbeispiele
Im Bereich des maschinellen Lernens ist das Steigungsdreieck besonders relevant. Es wird in neuronalen Netzwerken genutzt, um während des Trainings die Modelgewichte anzupassen. Der dabei berechnete Gradient, basierend auf der Steigung, wird durch das Steigungsdreieck bestimmt. Differentialrechnung findet auch in Regressionsmodellen Anwendung, zur Ermittlung optimaler Parameter, die eine Modellkurve den Daten bestmöglich annähern.
Minimierungsalgorithmus zur Kostenfunktion
Der Gradientenabstieg ist ein leistungsfähiger Weg, die Kostenfunktion zu senken. Diese Funktion bewertet den Unterschied zwischen vorhergesagten und echten Werten. Man bezeichnet diesen Unterschied häufig als Loss-Funktion. Mit jedem Schritt des Verfahrens versucht man, dieses Missverhältnis zu verringern. Dadurch verbessert sich die Genauigkeit des Machine-Learning-Modells.
Die Hauptstärke des Gradientenabstiegs liegt in der stetigen Verringerung des Fehlers. Das kontinuierliche Minimieren der Kostenfunktion führt zu effizienterem Training von Modellen. So lassen sich genauere Vorhersagen erzielen. Die Feinjustierung der Parameter in kleinen Etappen führt zu schrittweiser Kostenreduktion. Das ermöglicht es, die beste Lösung zu finden.
Die Rolle der Ableitung im Gradientenabstieg
Im Kern des Gradientenabstiegs ist die Ableitung entscheidend, denn sie zeigt, wo es steil bergauf geht. Sie hilft bei der Bestimmung des Gradienten in der mathematischen Analyse. Dieser Gradientenvektor, bestehend aus den ersten Ableitungen, zielt immer auf den steilsten Anstieg ab.

Beim Gradientenabstieg nutzen wir die entgegengesetzte Richtung dieses Gradienten. Dies hilft, das tiefste Tal der Funktion zu finden. Man bewegt sich schrittweise dorthin, wo der Abstieg am größten ist. So nähert man sich dem Minimum der Kostenfunktion an, das erreicht werden soll.
Die mathematische Analyse erlaubt uns, Ableitungen und Gradienten präzise zu berechnen. Dadurch werden die Ergebnisse genauer und die Optimierung effizienter. Offenbar ist die Ableitung unerlässlich im Gradientenabstiegsprozess.
Konvergenz und Iteration im Gradientenabstieg
Der Gradientenabstieg ist in der Welt des maschinellen Lernens unerlässlich, um durch Minimierung der Kostenfunktion optimale Parameter zu finden. Es ist von Bedeutung, Konvergenz und den Iterationsprozess zu verstehen, um den Algorithmus effektiv zu nutzen.
Was ist Konvergenz?
Konvergenz im Rahmen des Gradientenabstiegs bedeutet, einen Punkt zu erreichen, an dem weitere Iterationen die Kostenfunktion nicht wesentlich verbessern. Das zeigt an, dass eine optimale Lösung oder ein Minimum gefunden wurde. Hier spielt die Effizienz des Algorithmus eine große Rolle, denn sie bestimmt die Schnelligkeit und Genauigkeit, mit der dieser Punkt erreicht wird.
Iterative Vorgehensweise
Der Prozess des Gradientenabstiegs verbessert durch ständiges Anpassen der Parameter schrittweise das Resultat. Jede Iteration bringt den Algorithmus seinem Ziel näher, die Konvergenz zu erreichen. Dies erhöht nicht nur die Effizienz des Algorithmus, sondern auch die Qualität der Ergebnisse.
Wichtigkeit der Lernrate im Gradientenabstieg
Die Lernrate spielt eine zentrale Rolle im Gradientenabstieg, indem sie die Größe der Schritte zur Parameteraktualisierung steuert. Nur die richtige Einstellung der Lernrate führt zu einer schnellen und effizienten Konvergenz. Andernfalls könnte das Modell stagnieren, ohne signifikante Verbesserungen zu erreichen.
Lernrate festlegen
Eine angemessene Lernrate zu finden, erfordert Ausgewogenheit. Zu hohe Lernraten können Oszillationen auslösen, die den Konvergenzprozess stören. Auf der anderen Seite führt eine zu niedrige Lernrate zu einer deutlichen Verlangsamung der Konvergenz. Es ist entscheidend, verschiedene Werte zu testen und die Modellleistung zu evaluieren, um die ideale Lernrate festzulegen.
Optimale Lösung finden
Die optimale Lösung zu finden, benötigt Geduld und eine systematische Herangehensweise. Eine sorgfältige Performance-Evaluierung hilft dabei zu verstehen, wie verschiedene Lernraten die Ergebnisse beeinflussen. Die korrekte Justierung der Lernrate als Hyperparameter ist entscheidend für die Leistungssteigerung des Modells.
Fazit
Wir haben den enormen Einfluss des Gradientenabstiegs auf die Effektivität maschineller Lernalgorithmen beleuchtet. Dieser Optimierungsalgorithmus ist entscheidend für die Erstellung präziser Modelle. Solche Modelle sind fähig, genaue Vorhersagen zu machen. Das Verständnis und die korrekte Anwendung dieses Algorithmus sind daher für Innovationen im maschinellen Lernen unerlässlich.
Die Stärke des Gradientenabstiegs liegt darin, Kostenfunktionen effizient zu minimieren und Modelle fortlaufend zu verfeinern. Die Bedeutung der Ableitung und der angemessenen Einstellung der Lernrate sind dabei nicht zu unterschätzen. Diese Elemente sind zentral für die Konvergenz und Verbesserung der Modelle. Eine gut angepasste Lernrate hebt die Effizienz und Wirksamkeit der Lernmodelle hervor.
Somit bleibt der Gradientenabstieg ein zentrales Instrument in der KI-Forschung und -Entwicklung. Durch die gezielte Anwendung dieser Methodik können Datenwissenschaftler das Potenzial ihrer Modelle voll ausschöpfen. Damit treiben sie konstante Innovationen im Bereich des maschinellen Lernens voran. Die fachgerechte Nutzung dieses Algorithmus ist und bleibt ein Schlüsselfaktor für die Entwicklung leistungsfähiger Vorhersagemodelle.

